Multi-Reader Multi-Case Analysis

MRMC(Multi-Reader Multi-Case) 분석을 이해하고, iMRMC package를 통해 예시를 살펴본다.

R
statistics
rpackage
iMRMC
Author

Donghyung Lee

Published

December 27, 2024

Background

AUC와 Mann-Whitney statistic 관계

두 그룹의 분포가 같은 지 다른 지 검정하기 위한 방법 중 Mann-Whitney U test라는 비모수검정법이 있다. 비모수적검정법이기에 population의 분포에 대한 가정을 하지 않는다. 첫 번째 그룹에서 i.i.d로 뽑은 표본 데이터가 \(X_1, X_2, …, X_n\)이고, 두 번째 그룹에서 i.i.d로 뽑은 표본 데이터가 \(Y_1, Y_2, …, Y_m\)이라고 하자. Mann-Whitney U test에서 Null hypothesis, Alternative hypothesis는 다음과 같다.

Null hypothesis

\(H_0\): 두 그룹의 분포가 동일하다.

Alternative hypothesis 대립가설은 다음 중 한 가지이다.

\(H_1\): 두 그룹의 분포가 다르다.

\(H_1\): 첫 번째 그룹의 분포가 두 번째 그룹의 분포보도 오른쪽에 있다.

\(H_1\): 첫 번째 그룹의 분포가 두 번째 그룹의 분포보도 왼쪽에 있다.

Mann-Whitney statistic은 다음과 같다.

\[ U = \sum_{i=1}^{n_1} \sum_{j=1}^{n_2} S(X_i, Y_j) = R_1 - \frac{n_1 (n_1 + 1)}{2} \]

\[ \text{단, } S(X, Y) = \begin{cases} 1 & \text{if } X > Y \\ \frac{1}{2} & \text{if } X = Y \\ 0 & \text{if } X < Y \end{cases} \]

\(R_1\)은 첫 번째 그룹의 순위합을 나타낸다.

이 때 U를 n1, n2로 나누어 정규화를 하면 그 값은 X > Y일 확률을 추정하는 통계량이 되며 이는 AUC의 값과 동일하다.

\[AUC = \frac{U}{n_1 n_2} = P(X > Y) + \frac{1}{2} P(X = Y) \]

시각적으로 왜 AUC와 정규화한 U statistic이 같은 지를 시각적으로 보여주는 그림이다. positive case와 negative case를 rank순으로 배치한 뒤, positive case만 모아 다시 그림을 그린다.

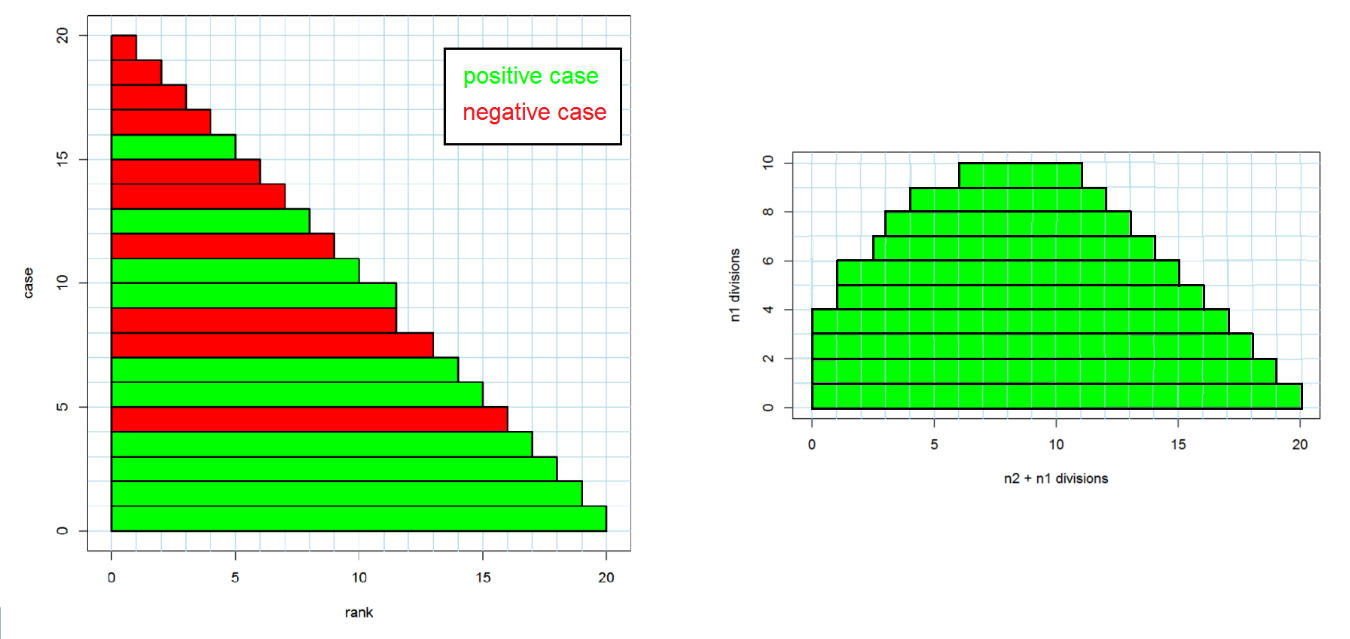
왼쪽 직사각형에 속하는 부분의 넓이가 U statistic이 되며 이를 n1과 n2로 나누어주면 AUC가 됨을 확인할 수 있다.

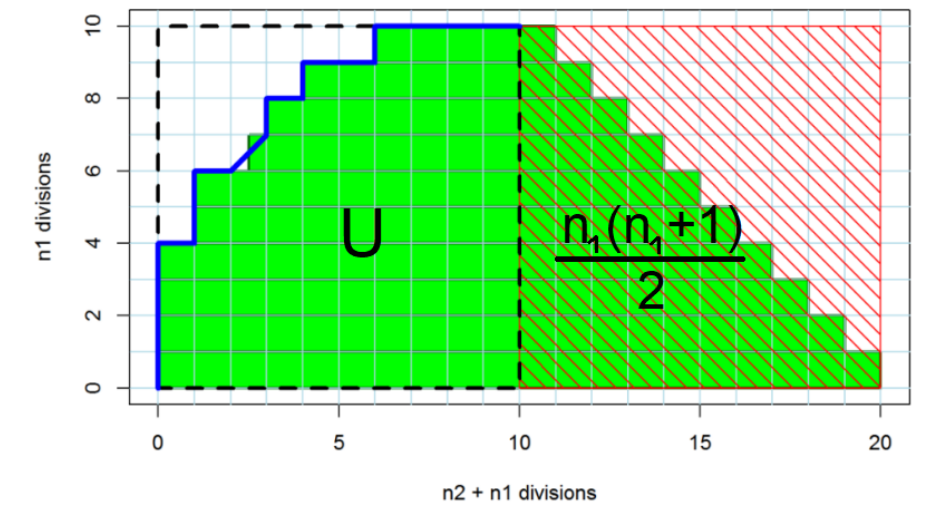
Motivation

새로운 영상 의학의 판독법의 효과를 종래의 판독법과 성능을 비교해야 하는 상황을 생각해보자. 영상 의학 검사는 reader마다 양성임을 판단하는 threshold가 다르기 때문에, sensitivity와 specificity의 variability가 다를 수 밖에 없다. 그렇기에 그런 효과를 보정하기 위하여 Multi-Reader Multi-Case analysis가 도입되었다. Each case는 multiple readers에 review되며, each reader는 multiple cases를 review한다. 통계적으로는 모형에서 case와 reader의 효과를 random factor로 처리하고, 그에 따라 각각의 variability를 설명할 수 있다.

different modality의 성능평가 뿐만 아니라, machine learning algorithm result도 비교할 수 있다.

Multi-Reader Multi-Case analysis

Single Reader의 경우 다음과 같이 AUC의 estimator를 구한다.

\[\hat{AUC}_r = \frac{1}{N_0 N_1} \sum_{k=1}^{N_1} \sum_{k'=1}^{N_0} S(X_{rk} - Y_{rk'})\] \(X_{rk}\)는 Signal-Present Scores, \(Y_{rk'}\)는 Signal-Absent Scores를 의미한다.

\[ 단, s(x) = \begin{cases} 1.0, & x > 0 \quad \text{Correct ranking} \\ 0.5, & x = 0 \\ 0.0, & x < 0 \quad \text{Incorrect ranking} \end{cases} \]

[^note1]### 따라서 Average Over Readers는 다음과 같이 구할 수 있다.

\[ \hat{AUC}_\cdot = \frac{1}{N_R N_0 N_1} \sum_{r=1}^{N_R} \sum_{k=1}^{N_1} \sum_{k'=1}^{N_0} S(X_{rk} - Y_{rk'}) \]

간단한 예시를 하나 살펴보자.

Truth는 질병이 있는 지 없는 지 정답을 의미한다.

이때 Blue Reader와 Red Reader는 양성일 score를 modality A와 modality B로 각 case마다 판독을 하여 점수를 매긴다.

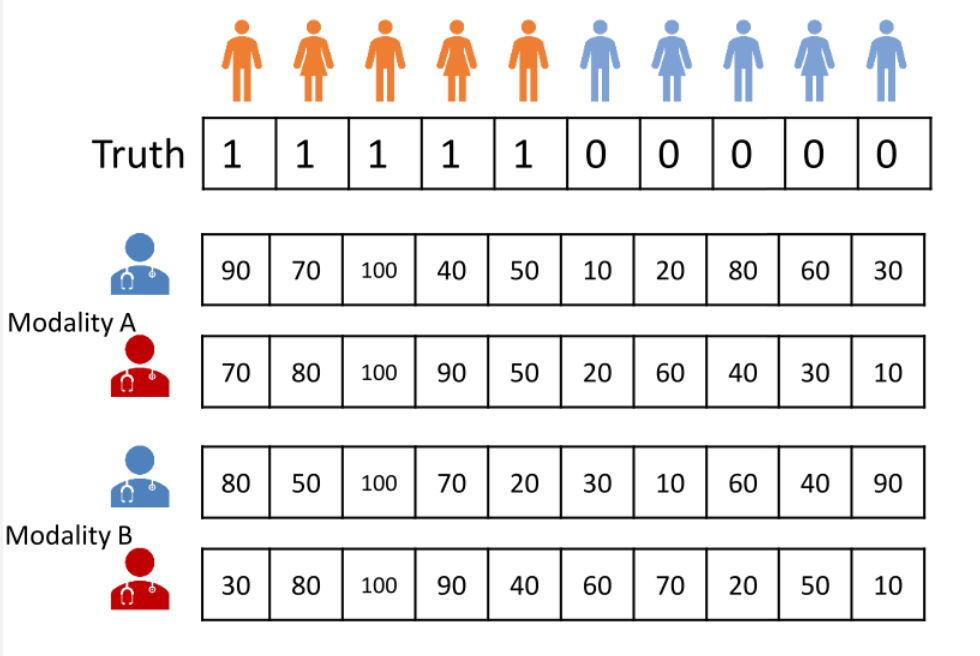
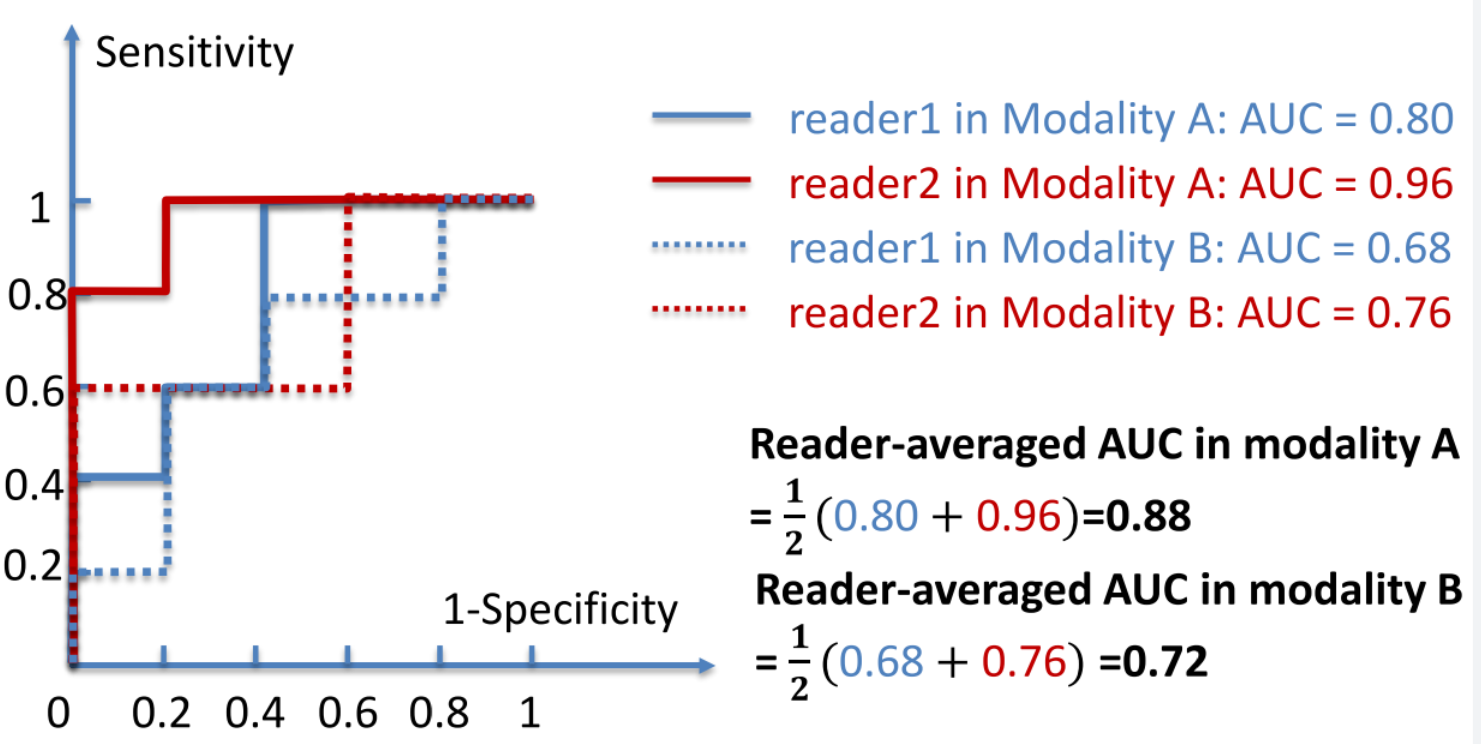
modality A와 modality B에 대해 각각의 mean AUC estimator를 구할 수 있다.

각 modality의 Reader-averaged AUC의 차이는 0.88 - 0.72 = 0.16 이 된다.

Variance of difference of reader-averaged AUC를 계산한다면 이 둘의 차이 여부에 대해 말할 수 있을 것이다.

Single Modality일 때, AUC estimator의 variance는 다음과 같이 7 terms로 나눌 수 있다.

\[ \text{var}(\hat{AUC}) = \frac{\sigma_0^2}{N_0} +\frac{\sigma_1^2}{N_1} +\frac{\sigma_{01}^2}{N_0 N_1} +\frac{\sigma_R^2}{N_R} +\frac{\sigma_{0R}^2}{N_0 N_R} +\frac{\sigma_{1R}^2}{N_1 N_R} +\frac{\sigma_{01R}^2}{N_0 N_1 N_R} \]

Each term이 의미하는 내용은 다음과 같다.

\(\frac{\sigma_0^2}{N_0}\): Normal Cases내 variability

\(\frac{\sigma_1^2}{N_1}\): Diseased Cases내 variability

\(\frac{\sigma_{01}^2}{N_0 N_1}\): Normal/Diseased cases사이 interaction에 의한 variability

\(\frac{\sigma_R^2}{N_R}\): Reader variabilty

\(\frac{\sigma_{0R}^2}{N_0 N_R}\): Normal case/Reader interaction에 의한 variability

\(\frac{\sigma_{1R}^2}{N_1 N_R}\): Diseased case/Reader interaction에 의한 variability

\(\frac{\sigma_{01R}^2}{N_0 N_1 N_R}\): Normal Case/Diseased Case/ Reader간 3중 interaction에 의한 variability

각 σ에 대한 정확한 계산식은 Clarkson et al. (2006)1을 참고하기 바란다.

Multi-Reader Multi-Case Simulation

연구비 절약, 윤리적 문제, case가 희귀한 경우, 새로운 의료 기기가 시장 출시되기 전 성능검증 등을 하기 위해 MRMC simulation할 수 있다. Roe and Metz model을 통해 data를 simulation 한다. 모형은 다음과 같다.

Roe and Metz model

\[X_{ijk}^{R\&M} = \mu_t + \tau_{it} + R_{jt} + C_{kt} + [RC]_{jkt} + [\tau R]_{ijt} + [\tau C]_{ikt} + [\tau RC]_{ijkt} + E_{ijkt}\]

이때, \(X_{ijk}\)에서 i는 modality, j는 reader, case는 k, t는 truth state를 의미한다. modality와 truth state는 fixed factor이고, reader와 case는 random factor이다. 이외 나머지 term들은 고유한 variance를 가진independent zero-mean Gaussian random variables이다.

iMRMC package

iMRMC는 MRMC analysis/simulation을 하기 위한 package로 다음의 주요한 2개의 function을 포함하고 있다.

  • doIMRMC: ROC data를 받아서 MRMC analysis를 수행하는 function

  • sim.gRoeMetz: MRMC data를 simulation하여 two modalities를 비교할 수 있는 function

cardiac CT study 예시 자료를 통해 MRMC를 수행해보자. colorScaleStudyData dataset은 다음 링크에서 다운로드 받을 수 있다.

이 study는 Grayscale, Rainbow and Hotiron등 세 가지의 modalities를 포함한다. 경험이 적은 판독자를 Low, 경험이 많은 판독자를 High로 표시하였으며, Low는 1~8까지 High는 1~4까지 총 12명의 판독자가 포함되어 있다. 총 210 cases를 포함하며, 그중 양성은 105개이다. 실습에 필요한 data는 cardioCTReaderData(판독자의 판독 결과)와 cardioCTGroundTruth data(정답)이다. 그리고 이 study는fully crossed가 아닌 split-plot study이다.

library(data.table); library(magrittr)
library(ggplot2); library(knitr)

load("data/cardioCTGroundTruth.rda")
load("data/cardioCTReaderData.rda")


setDT(cardioCTGroundTruth)
setDT(cardioCTReaderData)

cardioCTGroundTruth와 cardioCTReaderData는 다음과 같다.

names(cardioCTReaderData)[4] <- "score"
kable(cardioCTGroundTruth[1:30,], caption = "cardioCTGroundTruth", align = 'c' )
cardioCTGroundTruth
caseID truth
1 positive
2 positive
3 positive
4 positive
5 positive
6 positive
7 positive
8 positive
9 positive
10 positive
11 positive
12 positive
13 positive
14 positive
15 positive
16 positive
17 positive
18 positive
19 positive
20 positive
21 positive
22 positive
23 positive
24 positive
25 positive
26 positive
27 positive
28 positive
29 positive
30 positive 
kable(cardioCTReaderData[1:30,], caption = "cardioCTReaderData", align = 'c' )
cardioCTReaderData
readerID caseID modalityID score
Low1 141 Grayscale 31
Low1 142 Grayscale 54
Low1 143 Grayscale 88
Low1 144 Grayscale 88
Low1 145 Grayscale 54
Low1 146 Grayscale 32
Low1 147 Grayscale 55
Low1 148 Grayscale 33
Low1 149 Grayscale 66
Low1 150 Grayscale 99
Low1 151 Grayscale 75
Low1 152 Grayscale 54
Low1 153 Grayscale 21
Low1 154 Grayscale 66
Low1 155 Grayscale 88
Low1 156 Grayscale 22
Low1 157 Grayscale 42
Low1 158 Grayscale 76
Low1 159 Grayscale 32
Low1 160 Grayscale 75
Low1 161 Grayscale 65
Low1 162 Grayscale 65
Low1 163 Grayscale 55
Low1 164 Grayscale 32
Low1 165 Grayscale 52
Low1 166 Grayscale 77
Low1 167 Grayscale 20
Low1 168 Grayscale 87
Low1 169 Grayscale 65
Low1 170 Grayscale 42

cardioCTGroundTruth에 readerID와 modalityID columns를 추가하고 truth를 positive = 1, negative = 0이 되게끔 변형해준다.

cardioCTGroundTruth$readerID <- factor("truth")
cardioCTGroundTruth$modalityID <- factor("truth")
cardioCTGroundTruth$truth <- as.numeric(cardioCTGroundTruth$truth) -1 #truth는 factor형 pos: 2 neg: 1
names(cardioCTGroundTruth)[names(cardioCTGroundTruth) == "truth"] <- "score"

kable(cardioCTGroundTruth[1:30,], caption = "cardioCTGroundTruth", align = 'c' )
cardioCTGroundTruth
caseID score readerID modalityID
1 1 truth truth
2 1 truth truth
3 1 truth truth
4 1 truth truth
5 1 truth truth
6 1 truth truth
7 1 truth truth
8 1 truth truth
9 1 truth truth
10 1 truth truth
11 1 truth truth
12 1 truth truth
13 1 truth truth
14 1 truth truth
15 1 truth truth
16 1 truth truth
17 1 truth truth
18 1 truth truth
19 1 truth truth
20 1 truth truth
21 1 truth truth
22 1 truth truth
23 1 truth truth
24 1 truth truth
25 1 truth truth
26 1 truth truth
27 1 truth truth
28 1 truth truth
29 1 truth truth
30 1 truth truth

이제 cardioCTReaderData와 cardioCTGroundTruth dataset 두 개를 합쳐준다.

comb_data <- merge.data.frame(cardioCTGroundTruth, cardioCTReaderData, by = names(cardioCTReaderData), all = TRUE, sort = FALSE)
kable(comb_data[1:30,], caption = "combined dataset", align = 'c' )
combined dataset
readerID caseID modalityID score
truth 1 truth 1
truth 2 truth 1
truth 3 truth 1
truth 4 truth 1
truth 5 truth 1
truth 6 truth 1
truth 7 truth 1
truth 8 truth 1
truth 9 truth 1
truth 10 truth 1
truth 11 truth 1
truth 12 truth 1
truth 13 truth 1
truth 14 truth 1
truth 15 truth 1
truth 16 truth 1
truth 17 truth 1
truth 18 truth 1
truth 19 truth 1
truth 20 truth 1
truth 21 truth 1
truth 22 truth 1
truth 23 truth 1
truth 24 truth 1
truth 25 truth 1
truth 26 truth 1
truth 27 truth 1
truth 28 truth 1
truth 29 truth 1
truth 30 truth 1

이제 iMRMC 패키지를 불러오고 doIMRMC함수를 이용하여 MRMC analysis를 수행한다. iMRMC에선 Ustat은 non-parametric estimation에 의한 result를 나타내며, MLEstat은 각각 parameter의 maximum likelihood estimation을 나타낸다.

Warning: package 'iMRMC' was built under R version 4.4.2
result <- doIMRMC(data = comb_data)

AUCDf <- data.frame(rbind(result$MLEstat$AUCA[1:3],result$MLEstat$varAUCA[1:3], sqrt(result$MLEstat$varAUCA[1:3])),
row.names = c("AUC", "variance of AUC", "SE of AUC"))
names(AUCDf) <- result$MLEstat$modalityA[1:3]
kable(AUCDf, caption = "AUC for different modalities : MLEstat", align = 'c' )
AUC for different modalities : MLEstat
Grayscale Hot Rainbow
AUC 0.5902954 0.5671724 0.5176793
variance of AUC 0.0015535 0.0008297 0.0009073
SE of AUC 0.0394148 0.0288037 0.0301211 
AUCDf <- data.frame(rbind(result$Ustat$AUCA[1:3],result$Ustat$varAUCA[1:3], sqrt(result$Ustat$varAUCA[1:3])),
row.names = c("AUC", "variance of AUC", "SE of AUC"))
Warning in sqrt(result$Ustat$varAUCA[1:3]): NaNs produced
names(AUCDf) <- result$Ustat$modalityA[1:3] 
kable(AUCDf, caption = "AUC for different modalities : Ustat", align = 'c' )
AUC for different modalities : Ustat
Grayscale Hot Rainbow
AUC 0.5902954 0.5671724 0.5176793
variance of AUC 0.0010402 -0.0000249 0.0000338
SE of AUC 0.0322528 NaN 0.0058162

different modalities에 대해 AUC의 difference도 Ustat, MLEstat 두 가지 방법으로 estimation할 수 있다.

AUCDf <- data.frame(rbind(result$MLEstat$AUCAminusAUCB[4:6],result$MLEstat$varAUCAminusAUCB[4:6], sqrt(result$MLEstat$varAUCAminusAUCB[4:6]),
result$MLEstat$AUCAminusAUCB[4:6] - 1.96 * sqrt(result$MLEstat$varAUCAminusAUCB[4:6]), result$MLEstat$AUCAminusAUCB[4:6] + 1.96 * sqrt(result$MLEstat$varAUCAminusAUCB[4:6])), row.names = c("difference of AUC", "variance of difference of AUC", "SE of different of AUC", "95% CI lower bound", "95% CI upper bound"))

names(AUCDf) <- paste(result$MLEstat$modalityA[4:6], result$MLEstat$modalityB[4:6], sep = " vs. ") 
kable(AUCDf, caption = "Difference of AUC among different modalities : MLEstat", align = 'c' )
Difference of AUC among different modalities : MLEstat
Grayscale vs. Hot Grayscale vs. Rainbow Hot vs. Rainbow
difference of AUC 0.0231230 0.0726161 0.0494932
variance of difference of AUC 0.0021459 0.0024036 0.0019731
SE of different of AUC 0.0463239 0.0490261 0.0444191
95% CI lower bound -0.0676719 -0.0234750 -0.0375683
95% CI upper bound 0.1139178 0.1687072 0.1365547 
AUCDf <- data.frame(rbind(result$Ustat$AUCAminusAUCB[4:6],result$Ustat$varAUCAminusAUCB[4:6], sqrt(result$Ustat$varAUCAminusAUCB[4:6]),
                          result$Ustat$AUCAminusAUCB[4:6] - 1.96 * sqrt(result$Ustat$varAUCAminusAUCB[4:6]), 
                          result$Ustat$AUCAminusAUCB[4:6] + 1.96 * sqrt(result$Ustat$varAUCAminusAUCB[4:6])), 
                    row.names = c("difference of AUC", "variance of difference of AUC", "SE of different of AUC", "95% CI lower bound", "95% CI upper bound"))

names(AUCDf) <- paste(result$Ustat$modalityA[4:6], result$Ustat$modalityB[4:6], sep = " vs. ") 
kable(AUCDf, caption = "Difference of AUC among different modalities : Ustat", align = 'c' )
Difference of AUC among different modalities : Ustat
Grayscale vs. Hot Grayscale vs. Rainbow Hot vs. Rainbow
difference of AUC 0.0231230 0.0726161 0.0494932
variance of difference of AUC 0.0012101 0.0014347 0.0010837
SE of different of AUC 0.0347870 0.0378770 0.0329203
95% CI lower bound -0.0450596 -0.0016227 -0.0150307
95% CI upper bound 0.0913055 0.1468550 0.1140170

이제 Roe and Metz model을 사용하여, MRMC analysis simulation을 위한 dataset을 만들어보자. 이때 sim.gRoeMetz.config, sim.gRoemetz 두 함수를 이용하여, simulated dataset을 만들 수 있다.

sim.gRoeMetz.config 함수의 arguments는 다음과 같으며, 이를 통해 Roe and Metz model의 fixed/random effect를 조절할 수 있다.

sim.gRoeMetz.config의 argument를 통해 Roe and Metz model을 조절할 수 있다. sim.gRoemetz(config)함수는 sim.gRoeMetz.config를 통해 생성된 configuration object를 이용하여, simulated data를 생성한다.

config에 저장된 simulation parameter는 에 대한 자세한 설명은 iMRMC package확인할 수 있다.

이제, 이 두 함수를 이용하여 MRMC simulation을 수행한다.

library(ggplot2)

config <- sim.gRoeMetz.config() # Create a sample configuration file
df.MRMC <- sim.gRoeMetz(config) # Simulate an MRMC data set

이 두 함수를 통해 simulated dataset을 visualization 시켜보았다.

ggplot(subset(df.MRMC, modalityID %in% c("testA", "testB")),
       aes(x = score,
           color = factor(unlist(lapply(as.character(caseID),
                                        function(x) {strsplit(x, 'Case')[[1]][1]}))))) +
  geom_density(position = "identity", alpha = 0.2) +
  facet_grid(rows = "modalityID") +
  labs(x = "MRMC Reading Score", y = "Density") +
  theme(legend.title = element_blank())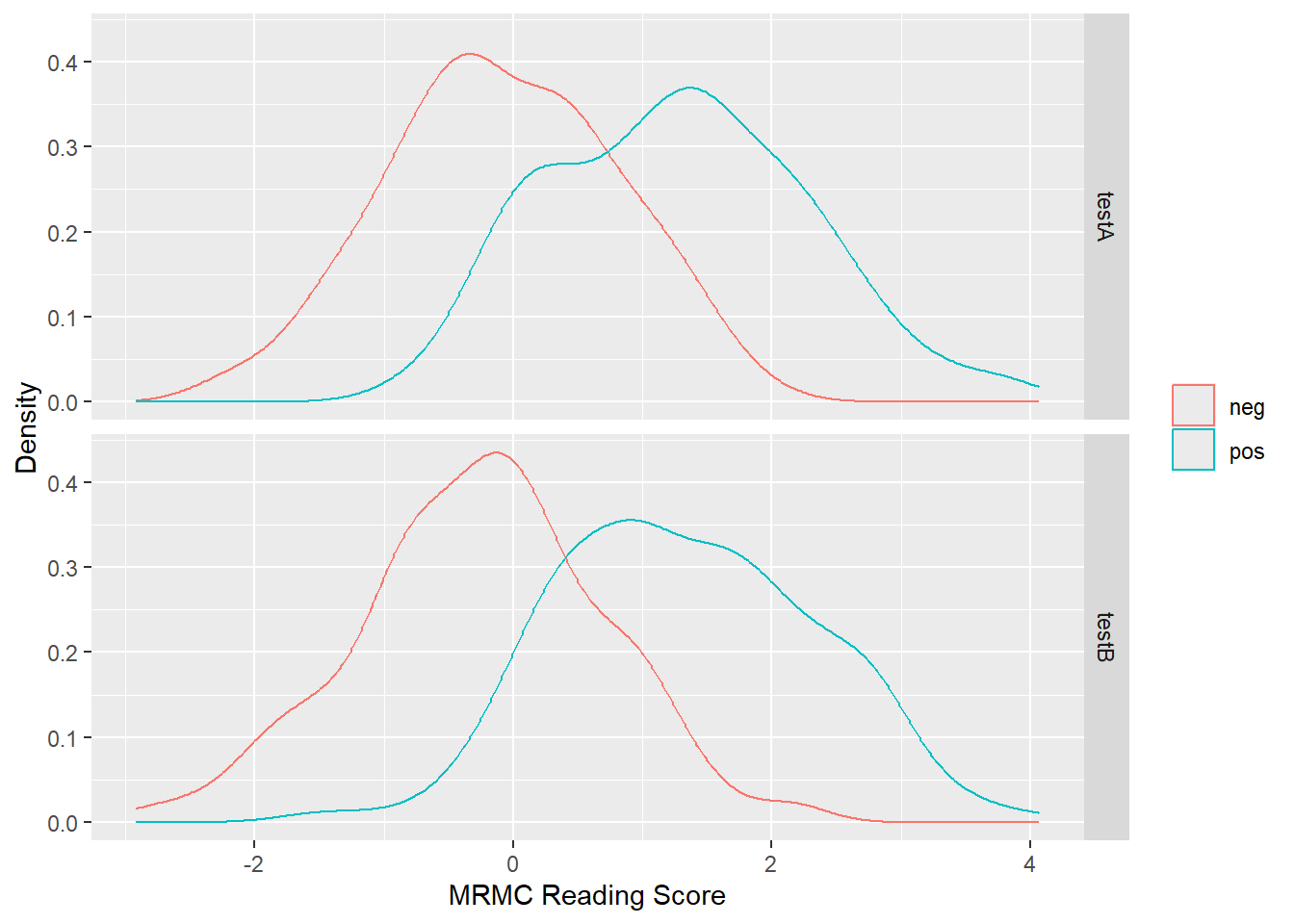

MRMC analysis를 수행해본 결과는 다음과 같다.

result <- doIMRMC(df.MRMC)

AUCDf <- rbind(result$MLEstat$AUCA[1:2],
      result$MLEstat$varAUCA[1:2],
      sqrt(result$MLEstat$varAUCA[1:2])) %>% as.data.frame()
rownames(AUCDf) <- c("AUC", "variance of AUC", "SE of AUC")
names(AUCDf) <- paste("test", c("A","B"))
AUCDf$`test A vs test B` <- c(result$MLEstat$AUCAminusAUCB[3], result$MLEstat$varAUCAminusAUCB[3], sqrt(result$MLEstat$varAUCAminusAUCB[3]))

kable(AUCDf, caption = "MRMC analysis result with simulated data : MLEstat", align = 'c')
MRMC analysis result with simulated data : MLEstat
test A test B test A vs test B
AUC 0.8411250 0.8797500 -0.0386250
variance of AUC 0.0016160 0.0011408 0.0024655
SE of AUC 0.0401991 0.0337760 0.0496538

Reference

  1. 박서영, & 김화영. (2023). 바이오통계학. 한국방송통신대학교출판문화원.
  2. Bischl et al. Chapter 04.13: AUC & Mann-Whitney-U Test Introduction to Machine Learning
  3. Wen et al. R Data Packages of Multi-Reader Multi-Case Studies and Simulation Tools to Support the Development of Reader Performance Evaluation Methods Wen
  4. Clarkson et al. (2006). A Probabilistic Model for the MRMC Method. Part 1. Theoretical Development. Acad Radiol.
  5. colorScaleStudyData

Footnotes

  1. Clarkson et al. (2006). A Probabilistic Model for the MRMC Method. Part 1. Theoretical Development. Acad Radiol.↩︎

Reuse

Citation

BibTeX citation:
@online{lee2024,
  author = {Lee, Donghyung},
  title = {Multi-Reader {Multi-Case} {Analysis}},
  date = {2024-12-27},
  url = {https://blog.zarathu.com/posts/2024-12-27-Multi-Reader Multi-Case Analysis},
  langid = {en}
}
For attribution, please cite this work as:
Lee, Donghyung. 2024. “Multi-Reader Multi-Case Analysis.” December 27, 2024. https://blog.zarathu.com/posts/2024-12-27-Multi-Reader Multi-Case Analysis.